Igualdades del máximo común divisor en loop

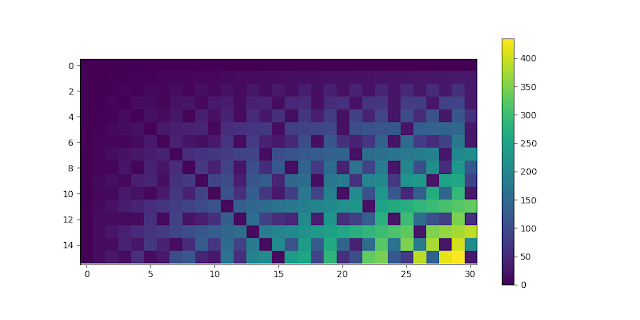
El código de color muestra el resultado de calcular el $gcd(x,y)$ para la $x$ en el eje
horizontal y la $y$ en el eje vertical. 

Como todos recordaréis el máximo común divisor (abreviado mcd o gcd, en inglés) de dos o más números enteros es el mayor número entero que los divide sin dejar residuo alguno. Por ejemplo  $gcd(6,9,18)=3$. En la figura del encabezado podéis ver el resultado del $gcd(x,y)$ para un pequeño conjunto de números.   Recordemos algunas de las propiedades básicas del máximo común divisor:    $$gcd(x,0)=|x|$$   $$gcd(mx,my)=mgcd(x,y)$$   $$gcd(x+my,y)=gcd(x,y)$$ donde $x,y,m$ son números enteros y $|x|$ representa el valor absoluto de $x$. Pues bien, aquí he demostrado que para seis números enteros positivos $a_1,b_1,a_2,b_2,a_3,b_3$ tales que  $$gcd(a_1,b_1)=gcd(a_2,b_2)=gcd(a_3,b_3)$$  entonces se cumple la siguiente igualdad:  $$gcd(d_{32},d_{21})=gcd(d_{32},d_{31})=gcd(d_{31},d_{21})$$ siendo $d_{ij}=|a_i{b}_j-a_j{b}_i|$. Vaya, una igualdad entre 3 gcds sobre 6 números implica otra igualdad entre también 3 gcds pero sobre otros 6 números construidos a partir de los 6 números iniciales.  Probemos los siguientes números,  $a_1=6,b_1=8,a_2=2$, $b_2=10$, $a_3=4$, $b_3=18$, dado que se cumple   $$gcd(6,8)=gcd(2,10)=gcd(4,18)=2$$ entonces para $d_{32}=|4\times 10-18\times 2|=4$, $d_{31}=|4\times 8-18\times 6|=76$ y $d_{21}=|2\times 8-10\times 6|=44$ se debe cumplir que  $$gcd(4,44)=gcd(4,76)=gcd(76,44)$$ que en efecto, como ya habréis verificado,  estos 3 gcds dan el mismo resultado, 4.

Ahora es cuando podemos comenzar el loop  asignando las $d_{ij}$ a las $a_i$ y las $b_i$ de la siguiente manera,   $$a_1=d_{32},b_1=d_{21},a_2=d_{32},$$ $$b_2=d_{31},a_3=d_{31},b_3=d_{21}$$ para poder confeccionar nuevos $d_{ij}$  y llegar a una nueva igualdad. Siguiendo el ejemplo anterior los nuevos $d_{ij}$ serían  $d_{32}=|76\times 76-4\times 44|=5600$, $d_{31}=|76\times 44-4\times 44|=3168$ y $d_{21}=|4\times 44-76\times 4|=128$ y la nueva igualdad es: $$gcd(5600,128)=gcd(5600,3168)=$$$$=gcd(3168,128)=32$$

Y el loop puede continuar hasta el infinito. Los siguientes $d_{ij}$ serían mucho mas grandes, $17335296,30954496,311296$, y los correspondientes gcds darían 19456. ¡Probad otros $a_i,b_i$ iniciales!

_________________________________________________________________________________

En verdad en el artículo mencionado, no sólo se asume que los gcds son iguales sino que son igual a 1:

$$gcd(a_1,b_1)=gcd(a_2,b_2)=gcd(a_3,b_3)=1$$

pero no es  necesario que sean igual a 1, cualquier otro valor mayor valdría. ¿Puedes demostrarlo?  

____________________________________________________________________________________________

Esta entrada participa en la Edición 11.6: Conjeturas del Carnaval de Matemáticas, que en esta ocasión organiza Gaussianos.